
1、(单选题) 食品厂加工某件产品,需要使用特定的包装袋,包装袋有大小两种规格,大的包装袋每袋能装23件产品,小的包装袋每袋能装6件产品,把133件产品装入包装袋内,要求每个包装袋都恰好装满,则最少需要的包装袋为多少个?
A 7
B 8
C 9
D 10
2、(单选题) 某校举行数理化竞赛,已知某高二年级参加数学竞赛的有49人,参加物理竞赛的有36人,参加化学竞赛的有28人,只参加其中两个科目的有13人,参加了全部科目的有9人,则参加此次数理化竞赛的总人数为( )人。
A 58
B 62
C 73
D 82
3、(单选题) 某公司A商品利润为定价的30%,前年销量为10万个;B商品利润为定价的40%,前年销量为4万个。去年公司将 A、B商品捆绑销售,售价为前年两种商品定价之和的90%,共卖出8万套,总利润比前年增加了20%。如两种商品去年的成本与前年相同,则前年A商品的定价为B商品定价的?
A 24%
B 25%
C 30%
D 36%
4、(单选题) 甲车间有3名钳工和4名车工,乙车间有5名钳工和4名电工。现从两个车间分别抽取2人组成一个工程小组,则工程小组恰有1名钳工和1名电工的概率接近:
A 0.56
B 0.32
C 0.16
D 0.04
5、(单选题) 3,5,4,8,4,10,( ),13
A 3
B 4
C 5
D 6
6、(单选题) 3,10,29,( ),127
A 44
B 52
C 66
D 78
7、(单选题) 2,5,10,17,( ),37
A 26
B 27
C 28
D 29
8、(单选题) 1995+1996+1997+1998+1999+2000值为:
A 12987
B 12985
C 11988
D 11985
9、(单选题) 一中学有10名数学老师,需抽调6人外出学习,但是张老师和李老师不能同时外出,则共有140种抽调方法。
A 正确
B 错误
10、(单选题) 小明只能记住妈妈手机号码的前7位,但他肯定,妈妈手机的后4位数全是奇数,最后一个数字是1,且后四位数中相邻数字均不相同,那么小明妈妈的手机号码有( )种可能。
A 27
B 48
C 64
D 80
答案解析...请翻下一页哦~

1、【答案】B
【解析】第一步,本题考查不定方程问题。
第二步,设大小包装袋分别有x、y个,则23x+6y=133,根据奇偶特性,得x为奇数,取值1、3、5······,要使包装袋最少,则x尽量大,当x=5时,115+6y=133,y=3,最少需要包装袋5+3=8个。
因此,选择B选项。
2、【答案】D
【解析】第一步,本题考查容斥问题,属于三集合容斥类。
第二步,根据三集合非标准型公式,参赛总人数=A+B+C-仅参加两个科目-2×三个科目都参加,可得参赛总人数=49+36+28-13-2×9=82人。
因此,选择D选项。
3、【答案】A
【解析】第一步,本题考查经济利润问题,属于利润率折扣类。
第二步,设A商品的定价为x,B商品的定价为y。则前年A商品的利润为0.3x,成本为0.7x;前年B商品的利润为0.4y,成本为0.6y。那么,去年的售价为(x+y)×90%=0.9x+0.9y,则去年的利润为(0.9x+0.9y)-(0.7x+0.6y)=0.2x+0.3y。
第三步,前年商品A销量为10万个,商品B销量为4万个,则前年总利润为(3x+1.6y)万;去年商品A、B绑定销售,销量B为8万套,则去年的总利润是(1.6x+2.4y)万;去年总利润比前年增加了20%,可知(1.6x+2.4y)=(1+20%)(3x+1.6y),化简得2x=0.48y,则x=0.24y。所以A商品的定价为B商品定价的24%。
因此,选择A选项。
4、【答案】C
【解析】第一步,本题考查概率问题,属于基本概率。
第二步,根据概率= 。总情况数为
。总情况数为 =756(种);要想满足题目条件,4人中1个电工、1个钳工,则剩下2人都是车工,而车工只有甲车间有,情况数为
=756(种);要想满足题目条件,4人中1个电工、1个钳工,则剩下2人都是车工,而车工只有甲车间有,情况数为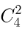 =6(种);再从乙车间选择1名钳工和1名电工,有
=6(种);再从乙车间选择1名钳工和1名电工,有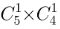 =20(种),故满足条件的情况数为6×20=120(种)。则满足条件的概率为
=20(种),故满足条件的情况数为6×20=120(种)。则满足条件的概率为 ≈0.158,最接近0.16。
≈0.158,最接近0.16。
因此,选择C选项。
5、【答案】C
【解析】第一步,本题考查数字推理,属于多重数列。
第二步,观察原数列项数较多且是共有8项,考虑两两分组得(3,5)、(4,8)、(4,10)、(( ),13),每组的两数之差形成的新数列为2、4、6,新数列是公差为2的等差数列,新数列下一项为6+2=8,原数列所求项为13-8=5。
因此,选择C选项。
6、【答案】C
【解析】解法一:
第一步,观察数列,每项数据皆在幂次数附近,考虑幂次修正数列。
第二步,数列可表示为幂次修正数列:1³+2,2³+2,3³+2,(4³+2),5³+2,底数是公差为1的等差数列,幂次数均为3,修正项均为2。所求项为:4³+2=66。
因此,选择C选项。
解法二:
第一步,数列变化趋势平缓,优先考虑做差。
第二步,做差如图所示:

猜测二级差数列是公差为6的等差数列,则下两项为12+6=18,18+6=24,差数列后两项为19+18=37,37+24=61,所求项为29+37=66,验证66+61=127,满足规律。
因此,选择C选项。
7、【答案】A
【解析】第一步,本题考查多级数列。
第二步,数列均匀递增,考虑做差。两两相减后差数列为3,5,7,(9),11,是公差为2的等差数列,故所求项应为17+9=26。
因此,选择A选项。
8、【答案】D
【解析】第一步,本题考查基础计算问题。
第二步,可用等差数列求和公式计算,可列式 。
。
因此,选择D选项。
9、【答案】A
【解析】第一步,本题考查排列组合问题,属于基础排列组合。
第二步,10名老师中抽调6人,方法有 种;若张老师和李老师同去,则需从其他8名老师中继续抽调4人,方法有
种;若张老师和李老师同去,则需从其他8名老师中继续抽调4人,方法有 种。所以张老师和李老师不同去的抽调方法有
种。所以张老师和李老师不同去的抽调方法有 -
- =140种。
=140种。
因此,判断本题正确。
10、【答案】C
【解析】第一步,本题考查排列组合问题,属于基础排列组合。
第二步,在0到9之间一共有5个奇数,由“最后一位确定是1,且后四位数中相邻数字均不相同”可得,倒数第二位有4种可能,倒数第三位有4种可能,倒数第四位也有4种可能。
第三步,根据乘法原理可得,共有4×4×4=64种可能。
因此,选择C选项。









